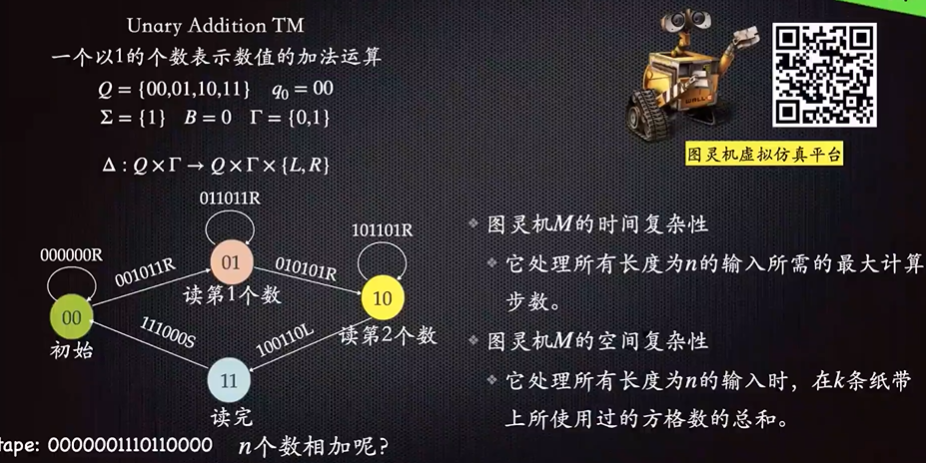
1 算法绪论
As n is finite, we talk about seconds,while as ,we talk about algorithm
与算法
算法的定义
- 问题(input,output)
- 状态转移指令(definite,finite)

-
解决问题的方法一定是算法吗?
-
枚举是不是算法?
严谨来说,不是算法,但是有策略的枚举就是算法,比如基于递归函数的枚举(回溯)、基于限界函数的枚举(分支限界)
-
拟合数据的AI模型是不是算法?
不是算法,AI模型的训练方法才是算法,缺乏确定的指令。
-
-
输入的问题:

-
输出的问题:

-
指令的问题:


算法是通过给定的一个无限性(数学)问题的实例(物理),在有限的次数内执行(算法计算模型)
算法的执行本质:
- 递归(一颗结满函数的递归树)
- 自动机(一个布满状态的有向图)
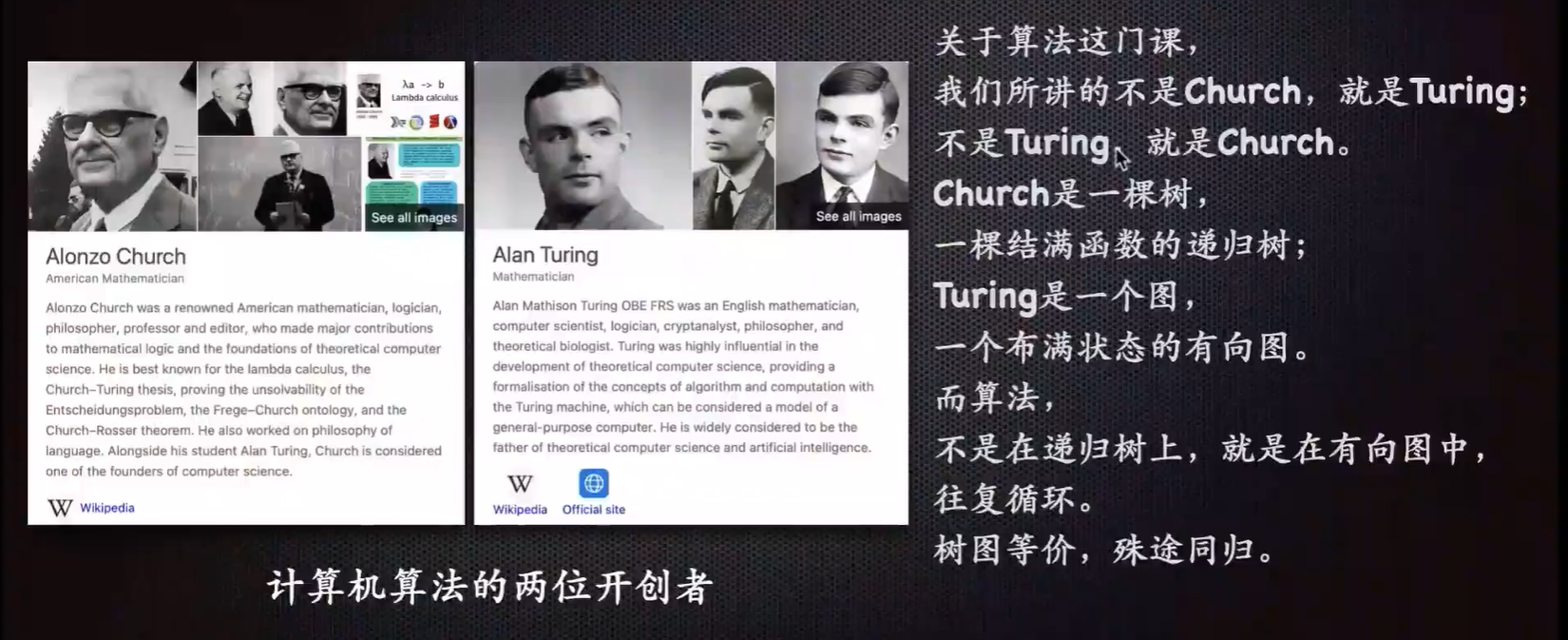
递归与图灵机
递归
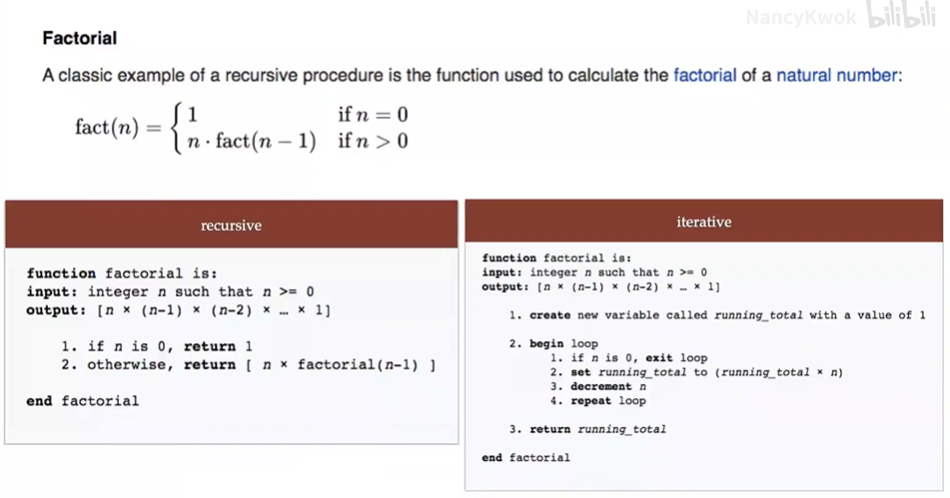
图灵机
有限状态机+无限长的纸带
- 是非空有穷状态集合
- 是非空有穷输入字母表,且不含包特殊的空符号(blank symbol)
- 是磁带的字母表,且
- 是转换函数,其中表示读写头是向左移还是向右移, - 表示不移动;
- 是开始状态
- 是接受状态
- 是拒绝状态,且
 Turing 的论文ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM.pdf提出了图灵机。
Turing 的论文ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM.pdf提出了图灵机。
The "computable" numbers may be described briefly as the real numbers whose expressions as a decimal are calculable by finite means.
“可计算”数可以简单地描述为实数,其十进制表达式可以用有限的方法计算。
According to my definition, a number is computable if its decimal can be written down by a machine.
根据我的定义,一个数字是可计算的,如果它的小数可以被机器写下来。
For the present I shall only say that the justification lies in the fact that the human memory is necessarily limited
就目前而言,我只想说,人类记忆必然是有限的这一事实是其正当性的依据
通过状态的转移会记录”所有“的之前操作