1 线性表
在编程的时候要把自己的编写的代码置身于开发大型项目的子模块视角中,有利于提高自己宏观解决问题的能力,main只是你的测试。
线性表定义:零个或者多个数据元素的有限序列。
线性表元素的个数定义为线性表的长度,当时,称为空表。
对于一个非空的线性表或者线性结构,具有以下特点:
- 存在唯一的一个被称作“第一个”的数据元素。
- 存在唯一的一个被称作“最后一个”的数据元素。
- 除了第一个外,结构中的每个数据元素都有一个前驱。
- 除了最后一个外,结构中的每个数据元素都有一个后继。
线性表顺序存储
线性表的顺序存储结构是指用一段地址连续的存储单元依次存储线性表的数据元素。

线性表顺序存储结构
/* datatype类型根据实际情况而定,这里假设为int */
typedef int datatype;
typedef struct node_st{
datatype *data; // 数组存储数据元素,最大值为MAXSIZE。
int last; //线性表当前�长度
}sqlist;
线性表顺序存储常用操作
初始化线性表
/**
* @description: 指针函数初始化顺序线性表
* @param {int} n
* @return {sqlist} *
*/
sqlist *sqlist_create(int n)
{
sqlist *me = NULL;
//初始化存储空间
me = malloc(sizeof(*me));
//初始化线性表空间,按照给定的长度开辟
me->data = malloc(sizeof(datatype)*n);
if (me == NULL)
return NULL;
//线性表当前长度初始化为-1
me->last = -1;
return me;
}
/**
* @description: 不带返回值初始化顺序线性表,这里双指针**ptr的意思是对指针的地址进行改变
* @param {sqlist} **ptr
* @param {int} n
* @return {*}
*/
void sqlist_create1(sqlist **ptr,int n)
{
*ptr = malloc(sizeof(**ptr));
(*ptr)->data = malloc(sizeof(datatype)*n);
if (*ptr == NULL)
return;
(*ptr)->last = -1;
return;
}
以上两种方式都可以对顺序线性表进行初始化,关于定义函数的注意事项参见:指针与函数 的内存泄漏章节。
顺序表插入与删除
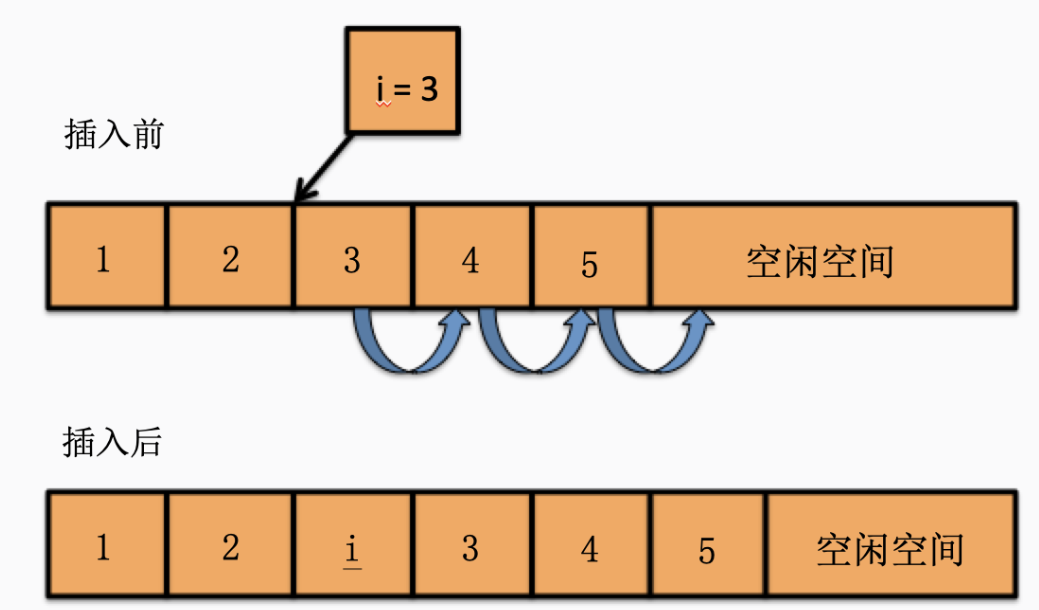
插入算法实现顺序:
- 如果插入位置不合理,抛出异常。
- 如果线性表长度大于等于数组长度,则抛出异常或者动态增加容量。
- 从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置。
- 将要插入的元素填入�到第i位置。
- 表长度加1。
/**
* @description: 线性表的插入
* @param {sqlist} *me
* @param {int} i
* @param {datatype} *data
* @return {*}
*/
int sqlist_insert(sqlist *me, int i, datatype *data)
{
int j;
//存储空间已满
if (me->last == DATASIZE - 1)
return -1;
//i值不合法判断
if (i < 0 || i > me->last + 1)
return -2;
for (j = me->last; i <= j; j--)
me->data[j + 1] = me->data[j];
//插入位置以及之后的位置后移动1位
me->data[i] = *data;
me->last++;
return 0;
}
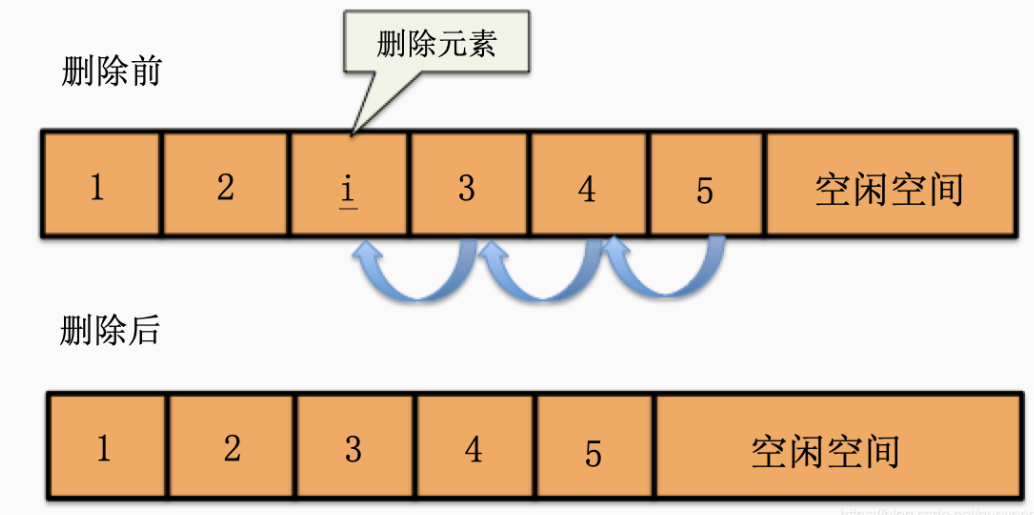
删除算法实现思路:
- 如果删除位置不合理,抛出异常。
- 取出删除元素。
- 从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置。
- 表长度减1。
/**
* @description: 线性表某个i位置元素进行删除
* @param {sqlist} *me
* @param {int} i
* @return {*}
*/
int sqlist_delete(sqlist *me, int i)
{
int j;
//判断i值是否合法
if (i < 0 || i > me->last)
return -1;
//从删除位置开始,将后面的元素都向前移动一位
for (j = i + 1; j <= me->last; j++)
me->data[j - 1] = me->data[j];
//更新线性表长度
me->last--;
//返回0表示删除成功
return 0;
}
其他线性表操作
获取指定元素的位置
/**
* @description: 查找匹配元素的位置下标
* @param {sqlist} *me
* @param {datatype} *data
* @return {int}
*/
int sqlist_find(sqlist *me, datatype *data)
{
int i;
//判断线性表是否为空
if (sqlist_isempty == 0)
return -1;
//遍历线性表,查找指定元素
for (i = 0; i < me->last; i++)
if (me->data[i] == *data)
return i;
//未找到指定元素,返回-2
return -2;
}
获取顺序表长度
/**
* @description: 查看线性表长度
* @param {sqlist} *me
* @return {int}
*/
int sqlist_getnum(sqlist *me)
{
return (me->last + 1);
}
判断顺序表是否为空表与清空
/**
* @description: 判断线性表是否为空
* @param {sqlist} *me
* @return {int}
*/
int sqlist_isempty(sqlist *me)
{
if (me->last = -1)
return 0;
return -1;
}
/**
* @description: 清空线性表
* @param {sqlist} *me
* @return {int}
*/
int sqlist_setempty(sqlist *me)
{
me->last = -1;
sqlist_destroy(me);
return 0;
}
顺序输出顺序表
/**
* @description: 显示线性表内容
* @param {sqlist} *me
* @return {void}
*/
void sqlist_display(sqlist *me)
{
int i;
if (me->last == -1)
return;
for (i = 0; i <= me->last; i++)
printf("%d ", me->data[i]);
printf("\n");
return;
}
线性表顺序存储的优缺点
优点:
- 无需为表示表中元素之前的逻辑关系增加额外的存储空间(相对与链式存储)。
- 可以快速地存取表中任一位置的元素。
缺点:
- 插入和删除元素操作需要移动大量的元素。
- 当线性表长度变化较大时,难以确定存储空间的容量。
- 造成存储空间的“碎片”。
全部代码
all : main # 默认目标是 main
main:main.o sqlist.o # main 依赖于 main.o 和 sqlist.o
$(CC) $^ -g -O0 -o $@ # 链接目标文件,生成可执行文件
clean: # 定义伪目标 clean
rm *.o main -rf # 删除所有目标文件和可执行文件
/*
* @Author: wrm244 wrm244@outlook.com
* @Date: 2023-06-22 16:37:43
* @LastEditors: wrm244 wrm244@outlook.com
* @LastEditTime: 2023-06-22 21:28:01
* @FilePath: /arr/sqlist.h
* @Description: 对顺序线性表的头文件,主要描述了线性表结构体与函数
*
* Copyright © 2023 by RiverMountain, All Rights Reserved.
*/
#ifndef sqlist_H__
#define sqlist_H__
#define DATASIZE 1024
typedef int datatype;
/**
* @description: 顺序线性表结构体包含元素指针与元素下标
* @param *data,last;
*/
typedef struct {
datatype *data;
int last;
}sqlist;
sqlist *sqlist_create(int);
void sqlist_create1(sqlist **,int);
int sqlist_insert(sqlist *,int i,datatype *);
int sqlist_delete(sqlist *,int i);
int sqlist_find(sqlist *,datatype *);
int sqlist_isempty(sqlist *);
int sqlist_setempty(sqlist *);
int sqlist_getnum(sqlist *);
int sqlist_union(sqlist *,sqlist*);
void sqlist_display(sqlist *);
int sqlist_destroy(sqlist *);
#endif
#include <stdio.h>
#include <stdlib.h>
#include "sqlist.h"
/**
* @description: 指针函数初始化顺序线性表
* @param {int} n
* @return {sqlist} *
*/
sqlist *sqlist_create(int n)
{
sqlist *me = NULL;
me = malloc(sizeof(*me));
me->data = malloc(sizeof(datatype)*n);
if (me == NULL)
return NULL;
me->last = -1;
return me;
}
/**
* @description: 不带返回值初始化顺序线性表,这里双指针**ptr的意思是对指针的地址进行改变
* @param {sqlist} **ptr
* @param {int} n
* @return {*}
*/
void sqlist_create1(sqlist **ptr,int n)
{
*ptr = malloc(sizeof(**ptr));
(*ptr)->data = malloc(sizeof(datatype)*n);
if (*ptr == NULL)
return;
(*ptr)->last = -1;
return;
}
/**
* @description: 对线性表的插入
* @param {sqlist} *me
* @param {int} i
* @param {datatype} *data
* @return {*}
*/
int sqlist_insert(sqlist *me, int i, datatype *data)
{
int j;
if (me->last == DATASIZE - 1)
return -1;
if (i < 0 || i > me->last + 1)
return -2;
for (j = me->last; i <= j; j--)
me->data[j + 1] = me->data[j];
me->data[i] = *data;
me->last++;
return 0;
}
/**
* @description: 线性表某个i位置元素进行删除
* @param {sqlist} *me
* @param {int} i
* @return {*}
*/
int sqlist_delete(sqlist *me, int i)
{
int j;
if (i < 0 || i > me->last)
return -1;
for (j = i + 1; j <= me->last; j++)
me->data[j - 1] = me->data[j];
me->last--;
return 0;
}
/**
* @description: 查找匹配元素的位置下标
* @param {sqlist} *me
* @param {datatype} *data
* @return {int}
*/
int sqlist_find(sqlist *me, datatype *data)
{
int i;
if (sqlist_isempty == 0)
return -1;
for (i = 0; i < me->last; i++)
if (me->data[i] == *data)
return i;
return -2;
}
/**
* @description: 判断线性表是否为空
* @param {sqlist} *me
* @return {int}
*/
int sqlist_isempty(sqlist *me)
{
if (me->last = -1)
return 0;
return -1;
}
/**
* @description: 清空线性表
* @param {sqlist} *me
* @return {int}
*/
int sqlist_setempty(sqlist *me)
{
me->last = -1;
return 0;
}
/**
* @description: 查看线性表长度
* @param {sqlist} *me
* @return {int}
*/
int sqlist_getnum(sqlist *me)
{
return (me->last + 1);
}
/**
* @description: 组合两个线性表返回给list1
* @param {sqlist} *list1
* @param {sqlist} *list2
* @return {int}
*/
int sqlist_union(sqlist *list1, sqlist *list2)
{
int i = 0;
while (i <= list2->last)
{
if (sqlist_find(list1, &list2->data[i]) < 0)
{
sqlist_insert(list1,i,&list2->data[i]);
}
i++;
}
}
/**
* @description: 显示线性表内容
* @param {sqlist} *me
* @return {void}
*/
void sqlist_display(sqlist *me)
{
int i;
if (me->last == -1)
return;
for (i = 0; i <= me->last; i++)
printf("%d ", me->data[i]);
printf("\n");
return;
}
/**
* @description: 销毁线性表内容
* @param {sqlist} *me
* @return {int} 成功返回0
*/
int sqlist_destroy(sqlist *me)
{
free(me);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "sqlist.h"
int main()
{
int i,err;
sqlist *list= NULL,*list1= NULL;
datatype arr[]={12,23,34,45,56};
datatype arr1[]={89,45,34,67,43,56,23};
//list = sqlist_create();
sqlist_create1(&list,6);
if(list == NULL)
{
fprintf(stderr,"sqlist_create() failed!\n");
exit(1);
}
list1 = sqlist_create(7);
if(list1 == NULL)
{
fprintf(stderr,"sqlist_create() failed!\n");
exit(1);
}
for(i = 0;i <sizeof(arr)/sizeof(*arr);i++)
{
if((err=sqlist_insert(list,0,&arr[i]))!=0)
{
if(err == -1)
fprintf(stderr,"The sqlist is full!\n");
else if(err ==-2)
fprintf(stderr,"The pos you want to insert is wrong\n");
else
fprintf(stderr,"Error!\n");
exit(1);
}
}
for(i = 0;i <sizeof(arr1)/sizeof(*arr1);i++)
{
if((err=sqlist_insert(list1,0,&arr1[i]))!=0)
{
if(err == -1)
fprintf(stderr,"The sqlist is full!\n");
else if(err ==-2)
fprintf(stderr,"The pos you want to insert is wrong\n");
else
fprintf(stderr,"Error!\n");
exit(1);
}
}
sqlist_display(list);
sqlist_display(list1);
//sqlist_destroy(list);
//sqlist_destroy(list1);
sqlist_union(list,list1);
sqlist_display(list);
exit(0);
}
线性表链式存储(非循环)
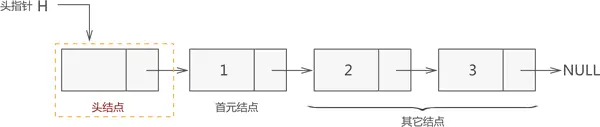
线性的链式存储结构(链表)是指用任意的存储单元来依次存放线性表的结点,这组单元既可以是连续的,也可以是不连续的,甚至是零散的分布在内存中的任意位置上。因此,链表中的结点的逻辑次序和物理次序不一定相同。为了正确表示结点间的逻辑结构,在存储每个结点值的同时,还必须存储指示其后继结点的地址(或位置)信息,这两部分组成了链表中的结点结构(如图)。
| data | next |
|---|
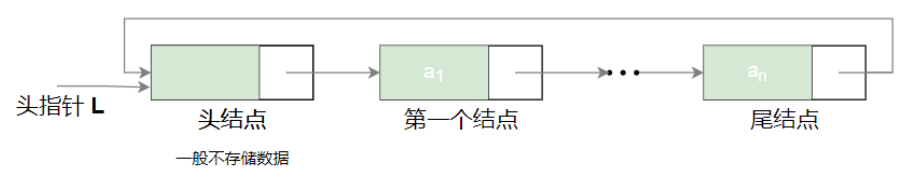
其中,data是数据域,用来存放结点的值。next是指针域(也称链域),用来存放后继结点的地址。链表正是通过每个结点的链域将线性表的n个结点按其逻辑次序连接在一起的。结点有一个链域的称为单链表。

线性表链式存储的优缺点
- 链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针
- 优点:插入或删除元素时很方便,使用灵活,存储空间利用率高。
- 缺点::存储密度小,查找和修改需要遍历整个链表。
- 顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一)﹔要求内存中可用存储单元的地址必须是连续的。优点:存储密度大,易于查找和修改。
- 缺点:插入或删除元素时不方便;存储空间利用率低,预先分配内存可能造成存储空间浪费。
线性表链式存储结构
/*
* @Author: wrm244 wrm244@outlook.com
* @Date: 2023-06-23 15:40:08
* @LastEditors: wrm244 wrm244@outlook.com
* @LastEditTime: 2023-06-23 19:10:52
* @FilePath: /list/linklist/simple/head/list.h
* @Description: 线性表的链式表示声明函数与数据结构
*
* Copyright © 2023 by RiverMountain, All Rights Reserved.
*/
#ifndef LIST_H__
#define LIST_H__
typedef int datatype; // 定义数据类型为整型
typedef struct list
{
datatype data; // 数据域
struct list *next; // 指针域,指向下一个节点
}list; // 定义链表结构体
list *list_create(); // 创建链表
int list_insert_at(list *,int ,datatype *); // 在指定位置插入元素
int list_order_insert(list *,datatype *); // 按顺序插入元素
int list_delete_at(list *,int i,datatype *); // 删除指定位置的元素
int list_delete(list *,datatype *); // 删除指定元素
int list_isempty(list *); // 判断链表是否为空
void list_display(list *); // 显示链表中的元素
void list_destroy(list *); // 销毁链表
#endif
需要注意的是:在函数定义的过程中如果需要传地址参数的话,尽量用void *func(type *,type *,...)来定义,而不是void *func(type &,type &,...),在标准C语言中是没有存在函数参数是&运算符,在C++中才有定义,然而这是国内数据结构和算法书籍的大多数写法或者说某些老师教学过程中把C与C++混为一谈,这是不可取的。另外一方面从逻辑上讲,试想以下,当你在阅读代码使用函数的情况下,不能根据外部输入判定我传进去的是什么类型参数,对于直觉来说是很不高效的。就比如说:
void func1(int *a)
{
*a = 100;
return ;
}
void func2(int &a)
{
a = 100;
return ;
}
int main(){
int *p = (int *)malloc(sizeof(int *)); //这里必须强转不然语义分析过不了。
*p = 10;
printf("[%s] *p=%d\n",__FUNCTION__,*p);
func1(p);
printf("[%s] f*p=%d\n",__FUNCTION__,*p);
}
/*输出结果
[main] *p=10
[main] f*p=100
*/
以上代码可以说我们在main函数中清楚明了知道p值是指针传进去给函数,函数收到的也是指针,不用再翻找fun1()函数的具体抽象定义,同样的如下代码:
void func2(int &a);
int main(){
int p = 10;
printf("[%s] p=%d\n",__FUNCTION__,p);
func2(p);
printf("[%s] fp=%d\n",__FUNCTION__,p);
}
/*输出结果
[main] p=10
[main] fp=100
*/
我们从以上代码的main()函数的变量定义可以看出,p就是int类型,不是指针,我引用func2()函数传进去也是int类型,但是实际上你还要去翻找该函数具体查看函数的抽象才能得知,这函数原来是把我传进去的变量给取了地址值,对我来说是比较不高效的。
含有空头节点链式存储
初始化链式线性表
/**
* @description: 初始化链式线性表
* @return {list} *
*/
list *list_create()
{
list *me;
me = malloc(sizeof(*me));
me->next = malloc(sizeof(*me));
if (me == NULL)
return NULL;
me->next = NULL; //头节点为空,下一链表地址赋值为空
return me;
}
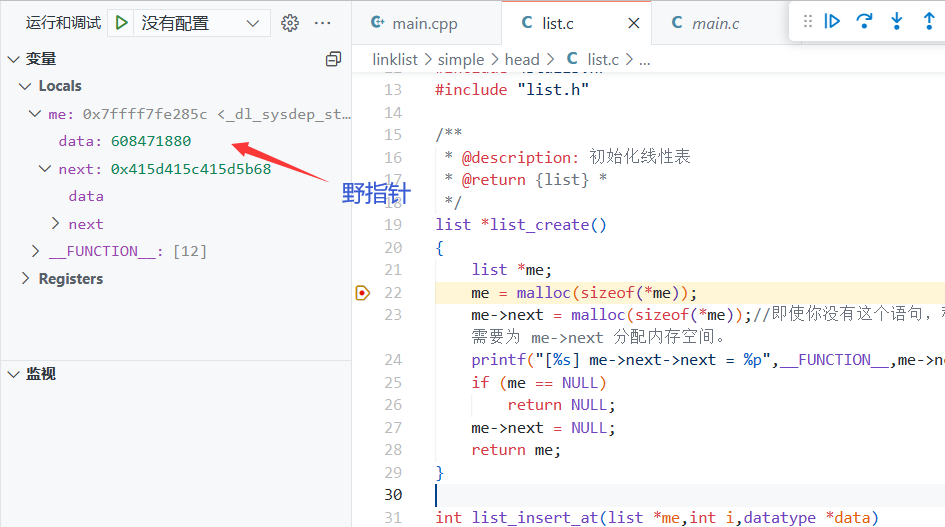
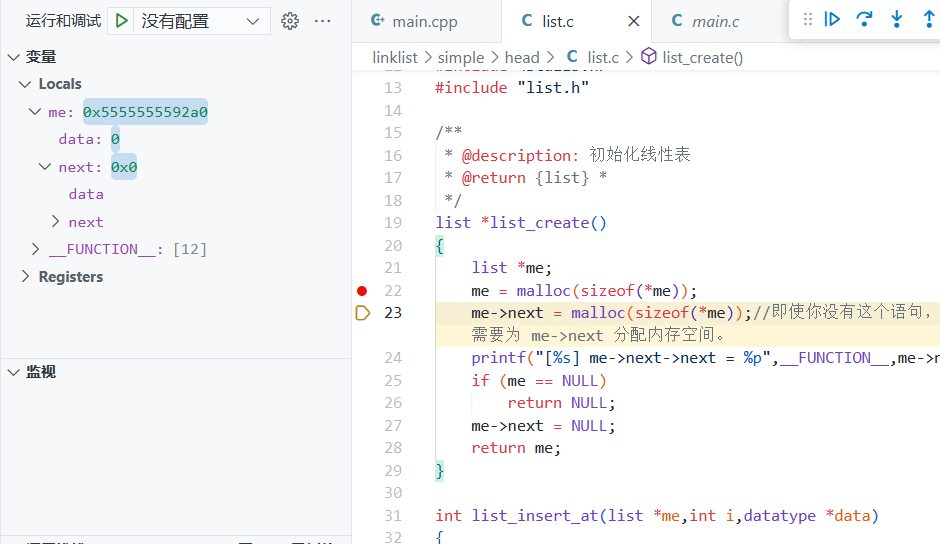
以上调试输出为[list_create] me->next->next = (nil) 即使你没有me->next = malloc(sizeof(*me));这个语句,程序也可能会执行成功(因为在申请结构体空间的时候,已经把me->next赋值为nil空指针,可以从调试上看得出来)。但是,这是不安全的,因为你不能时刻把握 me->next 是不是一个野指针,有可能在别的编译期中没有在初始化结构体的时候让其嵌套指针初始化。因此,建议为 me->next 分配内存空间。
插入与删除操作
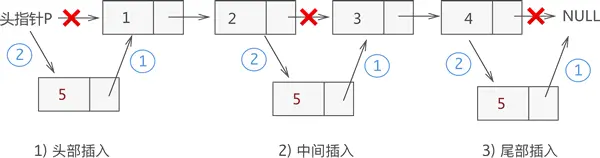
插入的两种操作
/**
* @description: 基于序列插入数值
* @param {list} *me
* @param {int} i
* @param {datatype} *data
* @return {int} 成功返回0,不成功返回其余值
*/
int list_insert_at(list *me,int i,datatype *data)
{
int j = 0;
list *node = me,*newnode; //代替me防止修改到原指针
if(i < 0)
return -1;
while(j < i && node != NULL){ //找去节点
node = node->next;
j++;
}
if(node){
newnode = malloc(sizeof(*newnode));
if(newnode == NULL)
return -2;
newnode->data = *data;
newnode->next = node->next; //这句话在第一次头节点next为空的情况下是废话
node->next = newnode;
return 0;
}else{
return -3;
}
}
/**
* @description: 插入的话区分上面尾插法头插法,在按顺序插入比较符合生产
* @param {list} *me
* @param {datatype} *data
* @return {int} 成功返回0,不成功返回其余值
*/
int list_order_insert(list *me,datatype *data)
{
list *p = me,*q;
while(p->next && p->next->data < *data) //找到前指针
p = p->next;
q = malloc(sizeof(*q));
if(q == NULL)
return -1;
q->data = *data;
q->next = p->next;
p->next = q;
return 0;
}
删除操作

int list_delete(list *me, datatype *data) {
list *p = me, *q;
while (p->next && p->next->data != *data) // 找到相等的前驱结点
p = p->next;
if (p->next == NULL)
return -1;
else {
q = p->next;
p->next = q->next;
free(q);
q = NULL;
}
return 0;
}
这种情况不保证删除重复元素
int list_delete_at(list *me, int i, datatype *data) {
int j = 0;
list *p = me, *q;
if (i < 0)
return -1;
while (j < i && p) {
p = p->next;
j++;
}
if (p) {
q = p->next;
*data = q->data;
p->next = q->next;
free(q);
q = NULL;
return 0;
}
return -2;
}
无空头节点链式存储
插入与删除操作
int list_insert(struct node_st **list, datatype *data) {
struct node_st *new;
new = malloc(sizeof(*new));
if (new == NULL)
return -1;
new->data = *data;
new->next = *list;
*list = new;
return 0;
}
int list_delete(struct node_st **list) {
struct node_st *cur;
if (*list == NULL) {
return -1;
}
cur = *list;
*list = (*list)->next;
free(cur);
return 0;
}
插入操作的过程和无头节点的区别是,需要注意引用的是链表的二级指针来实际操作链表,因为在有头结点时,你保留有这个链表的指针,插入只需提供指针变量即可。
销毁操作
int list_destroy(struct node_st *list)
{
struct node_st *cur;
if (list == NULL) {
return 0;
}
for (cur = list; cur != NULL; cur = list) {
list = cur->next;
free(cur);
}
return 0;
}
单链表应用举例
多项式合并
#include <stdio.h>
#include <stdlib.h>
struct node_st {
int coef;
int exp;
struct node_st *next;
};
struct node_st *poly_create(int a[][2], int n) {
struct node_st *me, *newnode, *cur;
int i;
me = malloc(sizeof(*me));
if (me == NULL) {
return NULL;
}
cur = me;
me->next = NULL;
for (i = 0; i < n; i++) {
newnode = malloc(sizeof(*newnode));
if (newnode == NULL)
return NULL;
newnode->coef = a[i][0];
newnode->exp = a[i][1];
newnode->next = NULL;
cur->next = newnode;
cur = newnode; // 向后移动链表
}
return me;
}
void poly_show(struct node_st *me) {
struct node_st *cur;
for (cur = me->next; cur != NULL; cur = cur->next) {
printf("(%d %d) ", cur->coef, cur->exp);
}
printf("\n");
}
void poly_union(struct node_st *p1, struct node_st *p2) {
struct node_st *p, *q, *r;
p = p1->next;
q = p2->next;
r = p1;
while (p && q) {
if (p->exp < q->exp) {
r->next = p;
r = p;
p = p->next;
} else if (p->exp > q->exp) {
r->next = q;
r = q;
q = q->next;
} else {
p->coef += q->coef;
if (p->coef) {
r->next = p;
r = p;
}
p = p->next;
q = q->next;
}
}
if (p == NULL) {
r->next = q;
} else {
r->next = p;
}
}
int main() {
int a[][2] = {{5, 0}, {2, 1}, {8, 8}, {3, 16}};
int b[][2] = {{6, 1}, {16, 6}, {-8, 8}};
struct node_st *p1, *p2;
p1 = poly_create(a, 4);
p2 = poly_create(b, 3);
poly_show(p1);
poly_show(p2);
/* poly_show(); */
poly_union(p1, p2);
poly_show(p1);
exit(0);
}
线性表链式循环存储
无头结点(约瑟夫问题)
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#define JOSE_NR 8
struct node_st {
int data;
struct node_st *next;
};
struct node_st *jose_create(int n) {
int i = 1;
struct node_st *me, *newnode, *cur;
me = malloc(sizeof(*me));
if (me == NULL)
return NULL;
me->data = i;
me->next = me; // 头节点环路
i++;
cur = me;
for (; i <= n; i++) {
newnode = malloc(sizeof(*newnode));
if (newnode == NULL) {
return NULL;
}
newnode->data = i;
newnode->next = me;
cur->next = newnode;
cur = newnode;
}
return me;
}
void jose_show(struct node_st *me) {
struct node_st *list;
for (list = me; list->next != me; list = list->next) {
printf("%d->", list->data);
/* sleep(1); */
/* fflush(NULL); */
}
printf("%d\n", list->data);
}
void jose_kill(struct node_st **me, int n) {
struct node_st *cur = *me, *node; // node是cur的前驱
int i = 1;
while (cur != cur->next) {
while (i < n) {
node = cur;
cur = cur->next;
i++;
}
printf("%d ", cur->data);
node->next = cur->next;
free(cur);
cur = node->next;
i = 1;
}
*me = cur;
printf("\n");
}
int main(int argc, char *argv[]) {
struct node_st *list;
int n = 3;
list = jose_create(JOSE_NR);
jose_show(list);
jose_kill(&list, n);
jose_show(list);
return EXIT_SUCCESS;
}
循环双链表(面向过程)
数据结构
struct llist_node_st
{
void * data; //void *,可以指向任何类型的数据
struct llist_node_st *prev;//指向前一个节点
struct llist_node_st *next;//指向后一个节点
};
typedef struct llist_head_st //链表头结构
{
int size;
struct llist_node_st head;
}LLIST;
函数抽象
typedef void llist_op(const void *);
typedef int llist_cmp(const void *,const void *);
LLIST* llist_create(int initsize);
void * llist_find(LLIST *, const void *key, llist_cmp *cmp);
int llist_insert(LLIST *, const void *data, int mode);//mode:0头插 1尾插
int llist_delete(LLIST *, const void *, llist_cmp *);
int llist_fetch(LLIST *, const void *, llist_cmp *,void *);
void llist_destory(LLIST *);
void llist_travel(LLIST *, llist_op *op);
各函数书写
LLIST* llist_create(int initsize){
LLIST *new;
new = malloc(sizeof(*new));
if(new == NULL)
return NULL;
new->size = initsize;
new->head.data=NULL;
new->head.prev=&new->head;
new->head.next=&new->head;//循环链表
}// 1.分配空间 2.初始化头节点 3.返回头节点地址
int llist_insert(LLIST *ptr, const void *data, int mode){
struct llist_node_st *newnode;
newnode = malloc(sizeof(*newnode));
if(newnode == NULL)
return -1;
newnode->data = malloc(ptr->size);
if(newnode->data == NULL){
free(newnode);
return -1;
}
memcpy(newnode->data, data, ptr->size);
if(mode == LLIST_FORWARD){//在头节点后前面插入
newnode->prev = &ptr->head;
newnode->next = ptr->head.next;
}else if(mode == LLIST_BACKWARD){ //在头节点前面插入
newnode->prev = ptr->head.prev;
newnode->next = &ptr->head;
}else{
return -3;
}
newnode->prev->next = newnode;
newnode->next->prev = newnode;
return 0;
}
void llist_destory(LLIST *ptr){
struct llist_node_st *cur,*next;
for(cur=ptr->head.next;cur!=&ptr->head;cur=next){//cur!=&ptr->head 保证了循环链表的遍历
next=cur->next;
free(cur->data);
free(cur);
}
free(ptr);
}
static struct llist_node_st* find_(LLIST *ptr,const void *key,llist_cmp *cmp){
struct llist_node_st *cur;
for(cur = ptr->head.next;cur!=&ptr->head;cur = cur->next){
if(cmp(key,cur->data)==0)
break;
}
return cur;
}
void * llist_find(LLIST *ptr, const void *key, llist_cmp *cmp){
return find_(ptr,key,cmp)->data;
}
int llist_delete(LLIST *ptr, const void *key, llist_cmp *cmp){
struct llist_node_st *node;
node = find_(ptr,key,cmp);
if(node == &ptr->head)
return -1;
node->prev->next = node->next;
node->next->prev = node->prev;
free(node->data);
free(node);
return 0;
}
int llist_fetch(LLIST *ptr, const void *key, llist_cmp *cmp,void *data){
struct llist_node_st *node;
node = find_(ptr,key,cmp);
if(node == &ptr->head)
return -1;
node->prev->next = node->next;
node->next->prev = node->prev;
if(data != NULL)
memcpy(data,node->data,ptr->size);
return 0;
}
void llist_travel(LLIST *ptr, llist_op *op){
struct llist_node_st *cur;
for(cur=ptr->head.next;cur!=&ptr->head;cur=cur->next){
op(cur->data);
}
}
循环双链(变长结构体)
结构体定义
struct llist_node_st
{
struct llist_node_st *prev;//指向前一个节点
struct llist_node_st *next;//指向后一个节点
char data[0]; //这个柔性数组,占位使用的。
};
typedef struct llist_head_st //链表头结构
{
int size;
struct llist_node_st head;
}LLIST;
柔性数组是和每个结构体绑定在一起的,而指针则不然,此外柔性数组在使用上是直接访问,形式上更加直观,而指针需要经过声明再进行动态分配内存,在效率上和柔性数组相比也稍微低一些。
循环双链表(面向对象)
结构体定义(类)
typedef struct llist_head //链表头结构
{
int size;
struct llist_node_st head;
int (*insert)(struct llist_head *,const void *,int);
void *(*find)(struct llist_head *,const void *,llist_cmp *);
int (*delete)(struct llist_head *,const void *,llist_cmp *);
int (*fetch)(struct llist_head *,const void *,llist_cmp *,void *);
void (*travel)(struct llist_head *,llist_op *);
}LLIST;
类的构造
LLIST* llist_create(int initsize){
LLIST *new;
new = malloc(sizeof(*new));
if(new == NULL)
return NULL;
new->size = initsize;
new->head.data=NULL;
new->head.prev=&new->head;
new->head.next=&new->head;//循环链表
new->insert=llist_insert;
new->find=llist_find;
new->delete=llist_delete;
new->fetch=llist_fetch;
new->travel=llist_travel;
}// 1.分配空间 2.初始化头节点 3.返回头节点地址