Skip to main content

二叉树

概述​

二叉树是这么一种树状结构：每个节点最多有两个孩子，左孩子和右孩子

二叉树​

重要的二叉树结构

  • 完全二叉树（complete binary tree）是一种二叉树结构，除最后一层以外，每一层都必须填满，填充时要遵从先左后右
  • 平衡二叉树（balance binary tree）是一种二叉树结构，其中每个节点的左右子树高度相差不超过 1

存储​

存储方式分为两种

  1. 定义树节点与左、右孩子引用（TreeNode）
  2. 使用数组，前面讲堆时用过，若以 0 作为树的根，索引可以通过如下方式计算
    • 父 = floor((子 - 1) / 2)
    • 左孩子 = 父 * 2 + 1
    • 右孩子 = 父 * 2 + 2

遍历​

遍历也分为两种

  1. 广度优先遍历（Breadth-first order）：尽可能先访问距离根最近的节点，也称为层序遍历
  2. 深度优先遍历（Depth-first order）：对于二叉树，可以进一步分成三种（要深入到叶子节点）
    1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树
    2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树
    3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

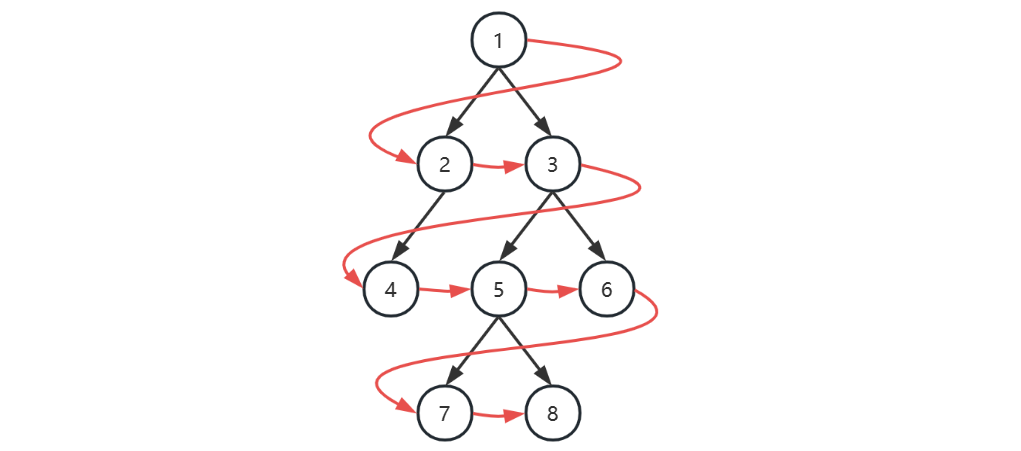
广度优先​

image-20230216153607396

本轮开始时队列本轮访问节点
[1]1
[2, 3]2
[3, 4]3
[4, 5, 6]4
[5, 6]5
[6, 7, 8]6
[7, 8]7
[8]8
[]
  1. 初始化，将根节点加入队列
  2. 循环处理队列中每个节点，直至队列为空
  3. 每次循环内处理节点后，将它的孩子节点（即下一层的节点）加入队列

注意

  • 以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树

  • 对于数组表现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

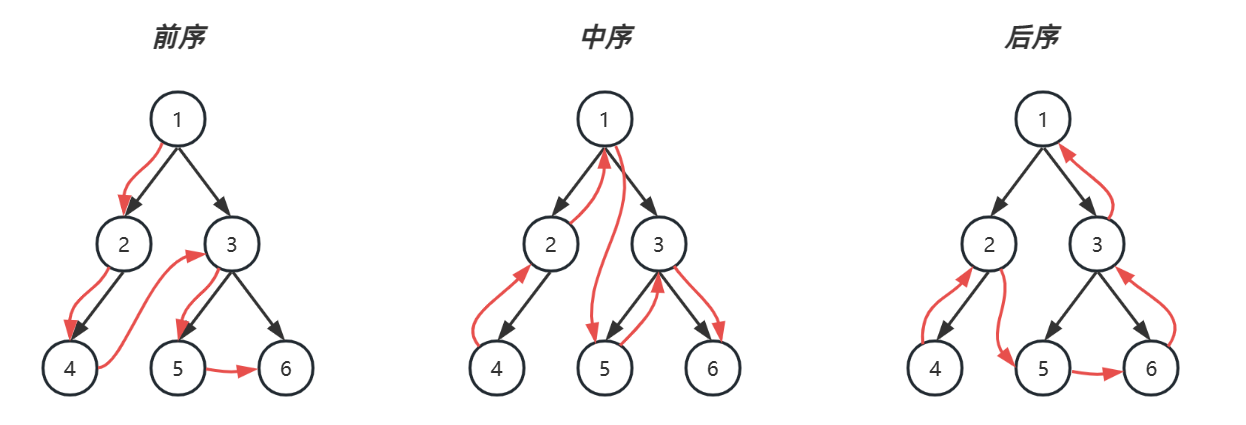
深度优先​

image-20230221110443230

栈暂存已处理前序遍历中序遍历
[1]1 ✔️ 左💤 右💤1
[1, 2]2✔️ 左💤 右💤
1✔️ 左💤 右💤		2
[1, 2, 4]4✔️ 左✔️ 右✔️
2✔️ 左💤 右💤
1✔️ 左💤 右💤		44
[1, 2]2✔️ 左✔️ 右✔️
1✔️ 左💤 右💤		2
[1]1✔️ 左✔️ 右💤1
[1, 3]3✔️ 左💤 右💤
1✔️ 左✔️ 右💤		3
[1, 3, 5]5✔️ 左✔️ 右✔️
3✔️ 左💤 右💤
1✔️ 左✔️ 右💤		55
[1, 3]3✔️ 左✔️ 右💤
1✔️ 左✔️ 右💤		3
[1, 3, 6]6✔️ 左✔️ 右✔️
3✔️ 左✔️ 右💤
1✔️ 左✔️ 右💤		66
[1, 3]3✔️ 左✔️ 右✔️
1✔️ 左✔️ 右💤
[1]1✔️ 左✔️ 右✔️
[]

递归实现​

/**
 * <h3>前序遍历</h3>
 * @param node 节点
 */
static void preOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.print(node.val + "\t"); // 值
    preOrder(node.left); // 左
    preOrder(node.right); // 右
}

/**
 * <h3>中序遍历</h3>
 * @param node 节点
 */
static void inOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    inOrder(node.left); // 左
    System.out.print(node.val + "\t"); // 值
    inOrder(node.right); // 右
}

/**
 * <h3>后序遍历</h3>
 * @param node 节点
 */
static void postOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    postOrder(node.left); // 左
    postOrder(node.right); // 右
    System.out.print(node.val + "\t"); // 值
}

非递归实现​

前序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        System.out.println(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        curr = pop.right;
    }

}

中序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        System.out.println(pop);
        curr = pop.right;
    }
}

后序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
TreeNode pop = null;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        if (peek.right == null || peek.right == pop) {
            pop = stack.pop();
            System.out.println(pop);
        } else {
            curr = peek.right;
        }
    }
}

对于后序遍历，向回走时，需要处理完右子树才能 pop 出栈。如何知道右子树处理完成呢？

  • 如果栈顶元素的 right≡nullright \equiv null 表示没啥可处理的，可以出栈

  • 如果栈顶元素的 right≠nullright \neq null，

    • 那么使用 lastPop 记录最近出栈的节点，即表示从这个节点向回走
    • 如果栈顶元素的 right==lastPopright==lastPop 此时应当出栈

对于前、中两种遍历，实际以上代码从右子树向回走时，并未走完全程（stack 提前出栈了）后序遍历以上代码是走完全程了

统一写法

下面是一种统一的写法，依据后序遍历修改

LinkedList<TreeNode> stack = new LinkedList<>();

TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {
    if (curr != null) {
        colorPrintln("前: " + curr.val, 31);
        stack.push(curr); // 压入栈，为了记住回来的路
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        // 右子树可以不处理, 对中序来说, 要在右子树处理之前打印
        if (peek.right == null) {
            colorPrintln("中: " + peek.val, 36);
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树处理完成, 对中序来说, 无需打印
        else if (peek.right == pop) {
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树待处理, 对中序来说, 要在右子树处理之前打印
        else {
            colorPrintln("中: " + peek.val, 36);
            curr = peek.right;
        }
    }
}

public static void colorPrintln(String origin, int color) {
    System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}

一张图演示三种遍历

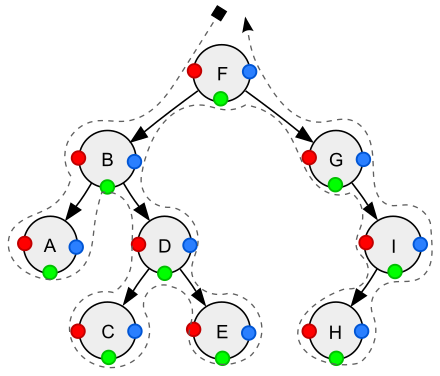
Sorted_binary_tree_ALL_RGB.svg

  • 红色：前序遍历顺序
  • 绿色：中序遍历顺序
  • 蓝色：后续遍历顺序
0%